Đề thi Toán lớp 7 năm 2024 (Đề số 1)

Để ôn luyện và làm tốt các bài thi Toán lớp 7, dưới đây là các Đề thi Toán 7 năm 2024 có đáp án, cực sát đề thi chính thức. Hi vọng bộ đề thi này sẽ giúp bạn ôn tập và đạt điểm cao trong các bài thi Toán 7.

I. TRẮC NGHIỆM (3 điểm)

Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.

Câu 1. Trong trò chơi gieo 2 đồng xu, các kết quả có thể xảy ra đối với mặt xuất hiện của đồng xu là 4. Nếu k là số kết quả thuận lợi cho biến cố thì xác suất của biến cố đó bằng

A. k

B. 2k

C. $\frac{k}{4}$

D. $\frac{4}{k}$

Câu 2. Biết 7x = 4y và y – x = 24. Khi đó, giá trị của x, y là

A. x = −56, y = −32;

B. x = 32, y = 56;

C. x = 56, y = 32;

D. x = 56, y = −32.

Câu 3. Diện tích xung quanh của khối gỗ có kích thước như sau:

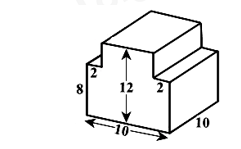
A. 44cm² B. 220cm² C. 440cm² D.22cm²

Câu 4. Cho x và y là hai đại lượng tỉ lệ nghịch với nhau và khi x = –12 thì y = 8. Khi x = 3 thì y bằng:

A. –32;

B. 32;

C. –2;

D. 2.

Câu 5. Biểu thức đại số biểu thị “Lập phương của hiệu của hai số x và y” là

A. x³ – y³;

B. (x – y)³;

C. x³ + y³;

D. (x + y)³.

Câu 6. Hệ số tự do của đa thức M = -8x² – 4x + 3 – 2x⁵là

A. -2;

B. 4;

C. 3;

D. 5.

Câu 7. Cho hai đa thức P(x) = 6x³ − 3x²− 2x + 4 và G(x) = 5x² − 7x + 9. Giá trị P(x) − G(x) bằng

A. x²− 9x +13;

B. 6x³ − 8x² + 5x −5;

C. x³ − 8x² + 5x −5;

D. 5x³ − 8x² + 5x +13.

Câu 8. Trong các giá trị sau đây, đâu là nghiệm của đa thức 5×2 − 3x – 2?

A. x = 1;

B. x = – 1;

C. x = $\frac{2}{5}$ ;

D. x = $\frac{{ - 2}}{5}$ .

Câu 9. Cho tam giác MNP có: \widehat N = 70^\circ ;\widehat P = 55^\circ . Khẳng định nào sau đây là đúng ?

A. MP < MN;

B. MP = MN;

C. MP > MN;

D. Không đủ dữ kiện so sánh.

Câu 10. Trong các khẳng định sau, khẳng định nào sai?

A. Hình lăng trụ đứng tam giác có 4 mặt, 6 đỉnh

B. Hình lăng trụ đứng tam giác có 5 mặt, 6 đỉnh

C. Công thức tính diện tích xung quanh của hình lăng trụ đứng tứ giác và tam giác là ${S_{xq}} = C.h$

D. Hình lăng trụ đứng tứ giác là lăng trụ đứng tứ giác có các mặt bên là các hình chữ nhật

Câu 11. Bộ ba độ dài đoạn thẳng nào sau đây không thể tạo thành một tam giác?

A. 18cm; 28cm; 10cm;

B. 5cm; 4cm; 6cm;

C. 15cm; 18cm; 20cm;

D. 11cm; 9cm; 7cm.

Câu 12. Cho tam giác ABC vuông tại A. Khẳng định nào dưới đây là đúng?

A. A là tâm đường tròn ngoại tiếp tam giác ABC.

B. A là trọng tâm tam giác ABC.

C. A là trực tâm tam giác ABC.

D. A là tâm đường tròn nội tiếp tam giác ABC.

II. PHẦN TỰ LUẬN (7,0 điểm)

Bài 1. (1,5 điểm) Tính chu vi của hình chữ nhật biết rằng chiều dài và chiều rộng của hình chữ nhật đó lần lượt tỉ lệ với 5,3 và hai lần chiều dài hơn ba lần chiều rộng là 8 cm.

Bài 2. (1,5 điểm) Cho hai đa thức:

$M\left( x \right) = 2 - 5{x^2} + 3{x^4} - 4{x^2} + 3x + {x^4} - 4{x^6} - 7x$

$N\left( x \right) = {\rm{ \;}} - 1 + 5{x^6} - 6{x^2} - 5 - 9{x^6} + 4{x^4} - 3{x^2}$

a) Thu gọn và sắp xếp các đa thức theo lũy thừa giảm dần của biến.

b) Tìm đa thức $H\left( x \right)$ và $G\left( x \right)$ biết $H\left( x \right) = M\left( x \right) + N\left( x \right)$ và $G\left( x \right) = M\left( x \right) - N\left( x \right).$

c) Tìm nghiệm của đa thức $G\left( x \right).$

Bài 3. (1,0 điểm) Chọn ngẫu nhiên một số trong tập hợp M = {2; 3; 5; 6; 8; 9}.

a) Trong các biến cố sau, biến cố nào là biến cố chắc chắn? Biến cố nào là biến cố không thể và biến cố nào là biến cố ngẫu nhiên?

A: “Số được chọn là số nguyên tố”;

B: “Số được chọn là số có một chữ số”;

C: “Số được chọn là số tròn chục”.

b) Tính xác suất của biến cố A.

Bài 4. (2,5 điểm) Cho tam giác ABC vuông tại A, đường phân giác BD (D∈AC). Từ D kẻ DH vuông góc với BC.

a) Chứng minh ΔABD = ΔHBD.

b) So sánh AD và DC.

c) Gọi K là giao điểm của đường thẳng AB và DH, I là trung điểm của KC. Chứng minh 3 điểm B, D, I thẳng hàng.

Bài 5. (0,5 điểm) Cho đa thức $f\left( x \right)$ thỏa mãn $f\left( x \right) + x.f\left( { - x} \right) = x + 1$ với mọi giá trị của x. Tính $f\left( 1 \right).$

Đáp án đề thi cuối kì 2 Toán 7 Kết nối tri thức

I. Trắc nghiệm

1.D	2.B	3. C	4.A	5.B	6. C
7.B	8.D	9.B	10.A	11.A	12.C

II. PHẦN TỰ LUẬN (7,0 điểm)

Câu 1

Gọi chiều dài và chiều rộng của hình chữ nhật lần lượt là x,y(cm) (điều kiện: x,y>0)

Theo đề bài: chiều dài và chiều rộng của hình chữ nhật đó lần lượt tỉ lệ với 5;3 nên ta có: $\frac{x}{5} = \frac{y}{3}$

Hai lần chiều dài hơn ba lần chiều rộng là 8 cm nên 2x – 3y = 8

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có: $\frac{x}{5} = \frac{y}{3} = \frac{{2x}}{{10}} = \frac{{3y}}{9} = \frac{{2x - 3y}}{{10 - 9}} = \frac{8}{1} = 8$

Khi đó, $\frac{x}{5} = 8 \Rightarrow x = 40$ (tmđk)

$\frac{y}{3} = 8 \Rightarrow y = 24$ (tmđk)

Chu vi của hình chữ nhật là: 2(x+y)=2(40+24)=128(cm)

Bài 2.

$M\left( x \right) = 2 - 5{x^2} + 3{x^4} - 4{x^2} + 3x + {x^4} - 4{x^6} - 7x$

$N\left( x \right) = {\rm{ \;}} - 1 + 5{x^6} - 6{x^2} - 5 - 9{x^6} + 4{x^4} - 3{x^2}$

a) Ta có:

$\begin{array}{*{20}{l}}{M\left( x \right) = 2 - 5{x^2} + 3{x^4} - 4{x^2} + 3x + {x^4} - 4{x^6} - 7x}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = {\rm{ \;}} - 4{x^6} + \left( {3{x^4} + {x^4}} \right) + \left( { - 5{x^2} - 4{x^2}} \right) + \left( {3x - 7x} \right) + 2}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = {\rm{ \;}} - 4{x^6} + 4{x^4} - 9{x^2} - 4x + 2}\end{array}$

$\begin{array}{*{20}{l}}{N\left( x \right) = {\rm{ \;}} - 1 + 5{x^6} - 6{x^2} - 5 - 9{x^6} + 4{x^4} - 3{x^2}}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = \left( {5{x^6} - 9{x^6}} \right) + 4{x^4} + \left( { - 6{x^2} - 3{x^2}} \right) + \left( { - 1 - 5} \right)}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = {\rm{ \;}} - 4{x^6} + 4{x^4} - 9{x^2} - 6}\end{array}$

b) Ta có:

$\begin{array}{*{20}{l}}{H\left( x \right) = M\left( x \right) + N\left( x \right)}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = ( - 4{x^6} + 4{x^4} - 9{x^2} - 4x + 2) + ( - 4{x^6} + 4{x^4} - 9{x^2} - 6)}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = \left( { - 4{x^6} - 4{x^6}} \right) + \left( {4{x^4} + 4{x^4}} \right) + \left( { - 9{x^2} - 9{x^2}} \right) - 4x + \left( {2 - 6} \right)}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = {\rm{ \;}} - 8{x^6} + 8{x^4} - 18{x^2} - 4x - 4}\end{array}$

$\begin{array}{*{20}{l}}{G\left( x \right) = M\left( x \right) - N\left( x \right)}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = ( - 4{x^6} + 4{x^4} - 9{x^2} - 4x + 2) - \left( { - 4{x^6} + 4{x^4} - 9{x^2} - 6} \right)}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = {\rm{ \;}} - 4{x^6} + 4{x^4} - 9{x^2} - 4x + 2 + 4{x^6} - 4{x^4} + 9{x^2} + 6}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = \left( { - 4{x^6} + 4{x^6}} \right) + \left( {4{x^4} - 4{x^4}} \right) + \left( { - 9{x^2} + 9{x^2}} \right) - 4x + \left( {2 + 6} \right)}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = {\rm{ \;}} - 4x + 8}\end{array}$

c) $G\left( x \right) = 0 \Rightarrow {\rm{ \;}} - 4x + 8 = 0 \Rightarrow {\rm{ \;}} - 4x = {\rm{ \;}} - 8 \Rightarrow x = 2.$

Bài 3. (1,0 điểm) M = {2; 3; 5; 6; 8; 9}.

a) Tập hợp M gồm có số nguyên tố và hợp số nên biến cố A là biến cố ngẫu nhiên.

Trong tập hợp M, tất cả các số đều là số có một chữ số nên biến cố B là biến cố chắc chắn.

Trong tập hợp M, không có số nào là số tròn chục nên biến cố C là biến cố không thể.

b) Trong tập hợp M gồm 6 số, có 3 số là số nguyên tố, đó là số 2; 3; 5.

Xác suất của biến cố A là: $\frac{3}{6}=\frac{1}{2}$

Bài 4. (2,5 điểm)

a) Xét DABD và ΔHBD có:

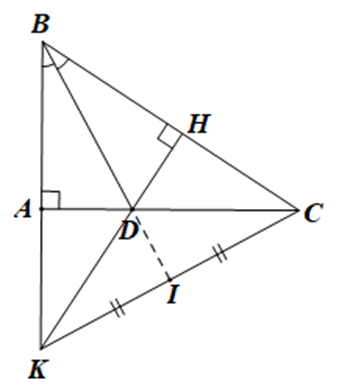
BAD^=BHD^=90°,

BD là cạnh chung,

$\widehat{ABD} = \widehat{HBD}$ (do BD là tia phân giác của ABD^).

Do đó ΔABD = ΔHBD (cạnh huyền – góc nhọn).

b) Từ ΔABD = ΔHBD (câu a) suy ra AD = HD (hai cạnh tương ứng)

Xét ΔDHC vuông tại H có DC là cạnh huyền nên DC là cạnh lớn nhất

Do đó DC > HD nên DC > AD.

c) Xét ΔBKC có CA ⊥ BK, KH ⊥ BC và CA cắt KH tại D

Do đó D là trực tâm của DBKC, nên BD ⊥ KC (1)

Gọi J là giao điểm của BD và KC.

Xét ∆BKJ và ∆BCJ có:

$\widehat{BJK} = \widehat{BJC}=90°,$

BJ là cạnh chung,

$\widehat{KBJ} = \widehat{CBJ}=90°$ ,(do BJ là tia phân giác của ABD^).

Do đó ΔBKJ = ΔBCJ (cạnh góc vuông – góc nhọn kề)

Suy ra KJ = CJ (hai cạnh tương ứng)

Hay J là trung điểm của KC.

Mà theo bài I là trung điểm của KC nên I và J trùng nhau.

Do đó ba điểm B, D, I thẳng hàng.

Bài 5.

+ Với x = – 1, ta có: $f\left( { - 1} \right) + \left( { - 1} \right).f\left( 1 \right) = - 1 + 1$

$\begin{array}{l} \Rightarrow f\left( { - 1} \right) - f\left( 1 \right) = 0\\ \Rightarrow f\left( { - 1} \right) = f\left( 1 \right)\end{array}$

+ Với x = 1, ta có: $f\left( 1 \right) + 1.f\left( { - 1} \right) = 1 + 1$

$\Rightarrow f\left( 1 \right) + f\left( { - 1} \right) = 2$

Suy ra, $f\left( 1 \right) + f\left( 1 \right) = 2$

$\begin{array}{l} \Rightarrow 2f\left( 1 \right) = 2\\ \Rightarrow f\left( 1 \right) = 1\end{array}$

Vậy $f\left( 1 \right) = 1$

Ma trận đề kiểm tra Toán học kì 2 KNTT

STT	Chương	Nội dung kiến thức	Mức độ kiến thức, kĩ năng cần kiểm tra, đánh giá								Tổng % điểm
			Nhận biết		Thông hiểu		Vận dụng		Vận dụng cao
			TN	TL	TN	TL	TN	TL	TN	TL
1	Tỉ lệ thức và đại lượng tỉ lệ	Tỉ lệ thức	1 (0,25đ)		1 (0,25đ)						17,5%
1	Tỉ lệ thức và đại lượng tỉ lệ	Tính chất dãy tỉ số bằng nhau và đại lượng tỉ lệ	1 (0,25đ)					1 (1,0đ)			17,5%
2	Biểu thức đại số và đa thức	Biểu thức đại số	1 (0,25đ)		1 (0,25đ)						32,5%
2	Biểu thức đại số và đa thức	Đa thức một biến	1 (0,25đ)			1 (1,0đ)		2 (1,0đ)		1 (0,5đ)	32,5%
3	Làm quen với biến cố và xác suất của biến cố	Biến cố		1 (0,75đ)							12,5%
3	Làm quen với biến cố và xác suất của biến cố	Xác suất của biến cố	1 (0,25đ)			1 (0,25đ)					12,5%
4	Quan hệ giữa các yếu tố trong một tam giác	Quan hệ giữa đường vuông góc và đường xiên. Các đường đồng quy của tam giác	3 (0,75đ)			1 (1,0đ)					32,5%
4	Quan hệ giữa các yếu tố trong một tam giác	Giải bài toán có nội dung hình học và vận dụng giải quyết vấn đề thực tiễn liên quan đến hình học				1 (1,0đ)		1 (0,5đ)			32,5%
5	Một số hình khối trong thực tiễn	Hình hộp chữ nhật và hình lập phương	1 (0,25đ)		1 (0,25đ)						5%
*Tổng: Số câu* *Điểm*			9 (2,25đ)	1 (0,75đ)	3 (0,75đ)	4 (3,25đ)		4 (2,5đ)		1 (0,5đ)	22 (10đ)
*Tỉ lệ*			30%		40%		25%		5%		100%
*Tỉ lệ chung*			70%				30%				100%